論理クイズとは…
論理的な思考力が求められるクイズです。
問題文をよく読んでしっかりと考えれば、答えは導き出せます。
問題
問題1

【問題】
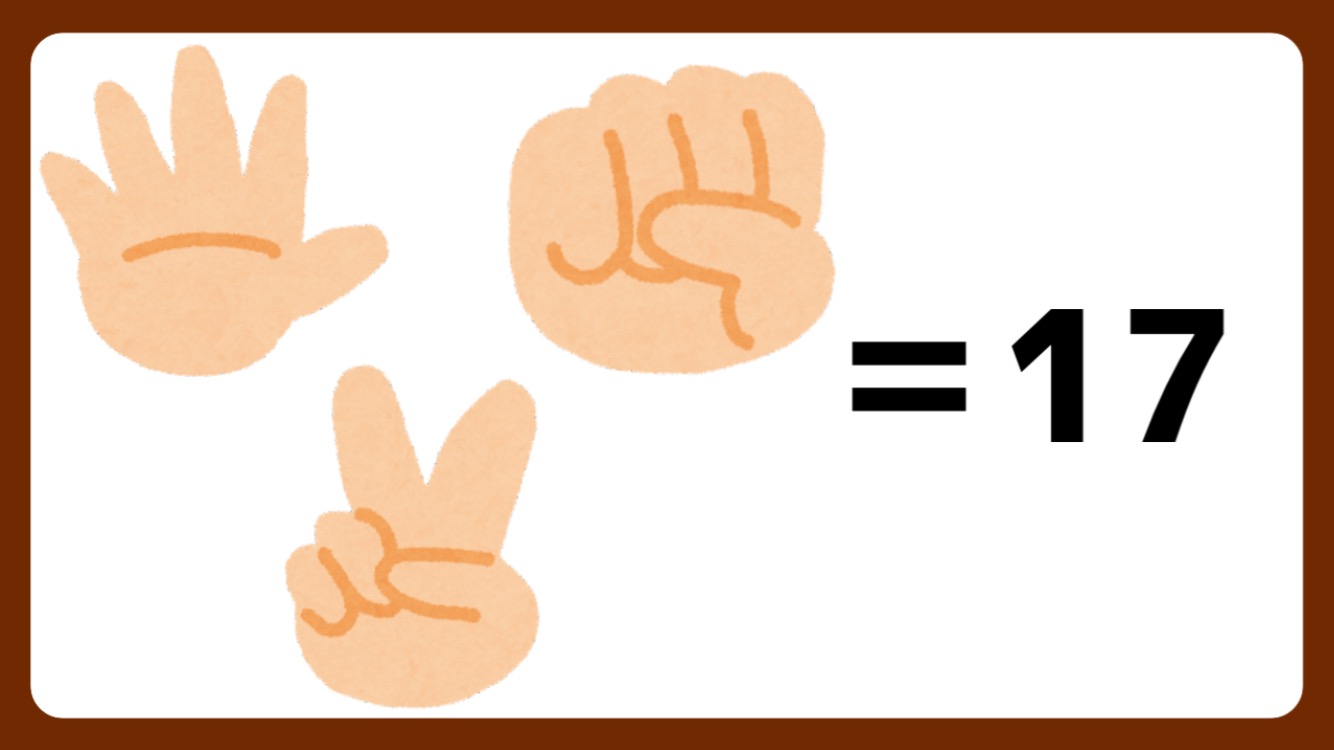
太郎くんはジャンケンを5回しました。
5回のじゃんけんで太郎くんが伸ばした指の本数が合計で17本だったとき、グー・チョキ・パーをそれぞれ何回ずつ出したでしょうか?
頭を少しひねって考えてみましょう!
下にスクロールすると「答え」があります。
グー=1回 チョキ=1回 パー=3回
解説
まずはジャンケンの指の本数を確認しましょう。
グー=0 チョキ=2 パー=5です。
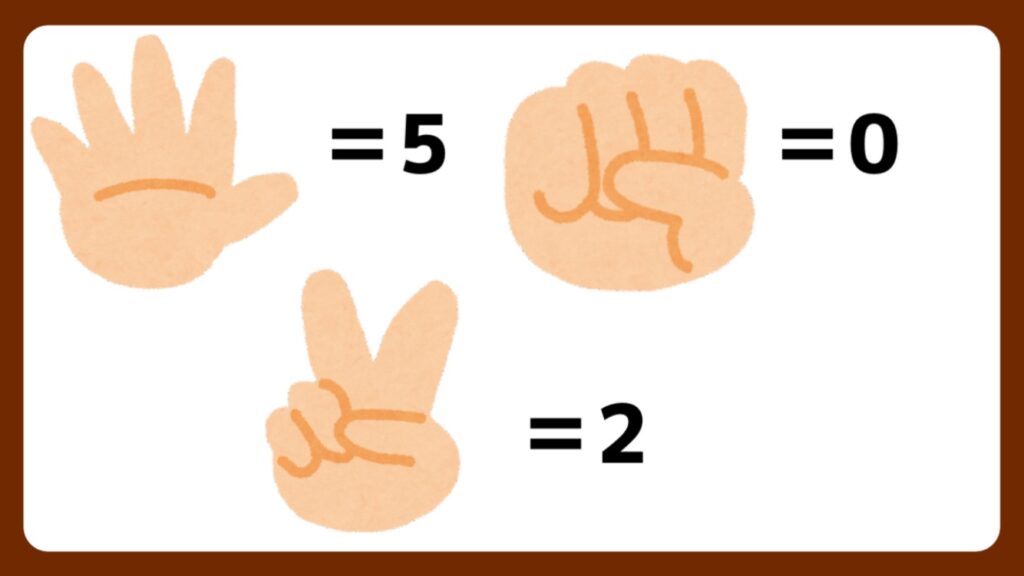
17は奇数なので、グー(0)とチョキ(2)のみではないことは確実です。少なくともパー(5)は1回以上出しているということになります。
パー(5)を1回しか出していない場合、残りの12はチョキ(2)を4回出しても(2×4=8で)12に届かないので誤りです。
では、パー(5)を2回ならどうでしょうか?
5×2=10で、残りは7ですが、これまた奇数なので、グー(0)とチョキ(2)のみでは7にすることはできません。
では、パー(5)を3回ならどうでしょうか?
5×3=15で、残りは2となり、この場合はチョキ(2)を1回出せば合計を17にすることができます。
ちなみにパー(5)を4回の場合、すでに5×4=20で17を超えているので、パー(5)を4回以上は全て誤りです。
以上のことから、グー=1回 チョキ=1回 パー=3回 が正解です。
(0×1+2×1+5×3=17)
問題2
それではもう一問。
【問題】
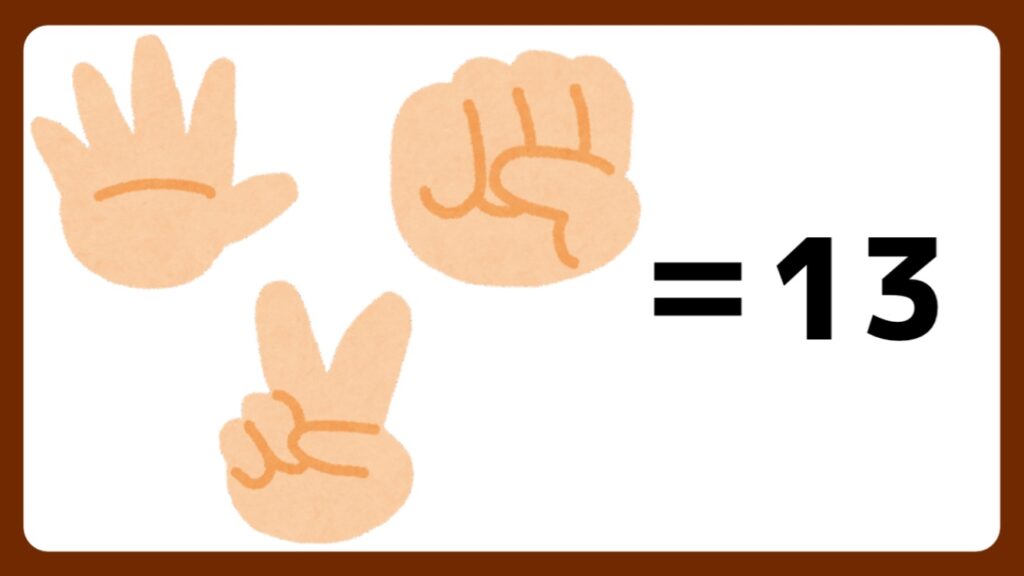
太郎くんはジャンケンを5回しました。
5回のじゃんけんで太郎くんが伸ばした指の本数が合計で13本だったとき、グー・チョキ・パーをそれぞれ何回ずつ出したでしょうか?
頭を少しひねって考えてみましょう!
下にスクロールすると「答え」があります。
グー=0回 チョキ=4回 パー=1回
解説
ジャンケンの指の本数は、グー=0 チョキ=2 パー=5です。
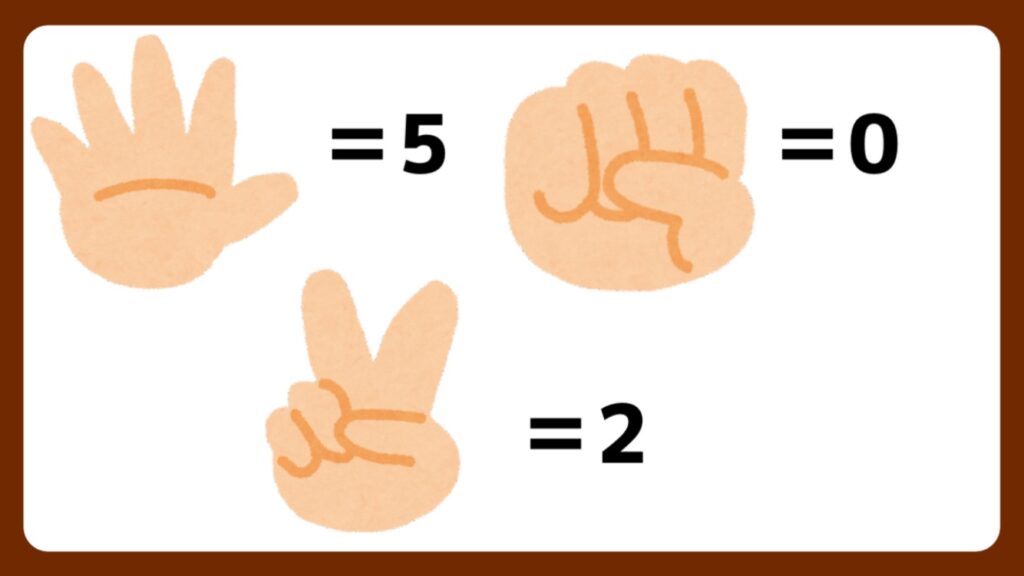
【問題1】と同様13は奇数なので、グー(0)とチョキ(2)のみではないことは確実です。少なくともパー(5)は一回以上出しているということになります。
パー(5)を1回しか出していない場合、残りは8であり、チョキ(2)を4回出せば(2×4=8で)合計を13にすることができます。
では、パー(5)を2回ならどうでしょうか?
5×2=10で、残りは3つまり奇数となります。グー(0)とチョキ(2)のみでは3にすることはできないので誤りです。
そして、パー(5)を3回の場合、すでに5×3=15で13を超えているので、パーが3回以上は全て誤りです。
以上のことから、グー=0回 チョキ=4回 パー=1回 が正解です。
(0×0+2×4+5×1=13)
おわりに
皆さまお疲れ様です。
何問解けましたか?
他にももっとクイズを楽しみたい方は、こちらもどうぞ↓